INTERPRETACION DE EVENTOS ALEATORIOS

Elementos básicos 

La probabilidad es la ciencia que trata de cuantificar los posibles resultados de un experimento en el cual está presente la incertidumbre o la aleatoriedad. La teoría de la probabilidad se usa extensamente en áreas como la estadística, la física, la matemática, la ciencia y la filosofía para sacar conclusiones sobre la probabilidad de sucesos potenciales y la mecánica subyacente de sistemas complejos.

En la teoría de la probabilidad, un evento aleatorio o fuente de sucesos aleatorio es un subconjunto de un espacio muestral, es decir, un conjunto de posibles resultados que se pueden dar en un experimento aleatorio. En teoría de la probabilidad a cada evento aleatorio se le puede asignar una medida de probabilidad, y el conjunto de todos los sucesos aleatorios constituye un álgebra de conjuntos.

Experimentos, Espacio muestral con y sin reemplazo y Eventos simples y compuestos. 

Primero necesitamos introducir algunos términos. Cuando trabajamos con probabilidad, una acción aleatoria o serie de acciones se llama experimento. Un resultado es la consecuencia de un experimento, y un evento es una colección particular de resultados. Los eventos usualmente son descritos usando una característica común de los resultados.

Ejemplo :

Algunos juegos requieren lanzar un dado de seis lados, numerado del 1 al 6. La tabla siguiente ilustra el uso de experimento, resultado, y evento en ese juego:

 Un evento simple es un evento con un solo resultado. Sacar un 1 sería un evento simple, porque existe sólo un resultado que funciona: 1. Sacar más que 5 también sería un evento simple, porque el evento incluye sólo al 6 como un resultado válido. Un evento compuesto es un evento con más de un resultado. Por ejemplo, lanzar un dado de 6 lados y sacar un número par: 2, 4, y 6.

Cuando lanzamos muchas veces un dado de 6 lados, no debemos esperar que un resultado ocurra más frecuentemente que otro. Los resultados en esta situación se dice que son igualmente probables. Es muy importante reconocer cuándo los resultados son igualmente probables cuando calculamos probabilidades. Como cada resultado en el experimento de lanzar los dados es igualmente probable, esperaríamos obtener cada resultado 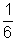 de los lanzamientos. Eso es, esperaríamos que salga 1 en  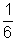de los lanzamientos, 2 en  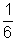de los lanzamientos, 3 en  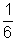de los lanzamientos y así sucesivamente.

Probabilidad de Eventos

La probabilidad de un evento es la frecuencia con que se espera que ocurra. Cuando todos los resultados posibles de un experimento son igualmente probables, la probabilidad es la relación entre el tamaño del espacio de eventos (los resultados en el evento) y el espacio muestral (todos los posibles resultados del experimento). La probabilidad de un evento E normalmente se escribe P(E).

EVENTOS

-Unión: se representa con el símbolo U

La unión entre dos conjuntos A y B, de define como los elementos que están en A, o están en B, se reprensenta por (AUB)

- Intersección.: se representa con el símbolo ∩

Se define como los elementos que están en A y en B (A∩B)

- Complemento

El complemento de un evento A se define como todos los elementos de Ω que no están en A. se representa como Ac , A-

- Eventos mutuamente excluyente (M.E):

 Los cuales A y B son M.E sino tienen puntos muéstrales en común.

Ejemplos:

1) La probabilidad de que un solo lanzamiento de un dado i) el resultado sea impar ii) el resultado sea un numero menor que 5. A:impar   B: numero menor que 5

P(A)= 36

P(B)= P(1)+ P(2)+ P(3)+ P(4)= 16+ 16 + 16 + 16=46 = 23

2) se lanza un dado la probabilidad de que resulte 3 o 6?

 Ω ={1,2,3,4,5,6} P(wi) donde i=1,..6 es 16

entonces la probabilidad de que salga 3 o 6 se escribe como 3 U 6 por lo tanto hallar P(3U6)

se puede notar que los eventos A y B son Independiente entonces P(A∩B)=0

P(3U6)=P(3)+P(6)= 16 + 16 =13

ejercicios relacionados: 

https://www.zweigmedia.com/MundoReal/tutorialsf15e/frames7_3b.html

Leyes:

- De adición.

La regla de la adición o regla de la suma establece que la probabilidad de ocurrencia de cualquier evento en particular es igual a la suma de las probabilidades individuales, si es que los eventos son mutuamente excluyentes, es decir, que dos no pueden ocurrir al mismo tiempo.

P(A o B) = P(A) U P(B) = P(A) + P(B) si A y B son mutuamente excluyente.

P(A o B) = P(A) + P(B) − P(A y B) si A y B son no excluyentes.

Siendo: P(A) = probabilidad de ocurrencia del evento A. P(B) = probabilidad de ocurrencia del evento B. P(A y B) = probabilidad de ocurrencia simultánea de los eventos A y B.

EJEMPLO :

 Supongamos que se extrae una carta de una baraja de 52 cartas. ¿Cuál es la probabilidad de que la carta sea o un rey o una figura negra? (Evento no mutuamente excluyente)

Solución: Hay 52 sucesos o eventos simples. Sean los sucesos o eventos

Hay 4 reyes. A = Que la carta sea un rey.

Hay 6 figuras negras            B = Que la carta sea una figura negra

P ( A U B ) =P( A ) + P( B ) – P( A ∩ B )

P(A U B)= 4/52 + 6/52 – 2/52 = 8/52= 0.15

- Condicional

La probabilidad condicional se calcula como el cociente entre la probabilidad conjunta y la probabilidad marginal del evento impuesto como condición. Si en un área determinada tomamos al azar un establecimiento agrícola entre aquellos que cultivan soja, la probabilidad de encontrar que cultiva maíz es una probabilidad condicional. Se trata de la probabilidad de cultive maíz bajo la condición de que el establecimiento sea uno que cultiva soja. Esta probabilidad toma el valor de la frecuencia relativa de establecimientos que cultivan maíz entre todos los establecimientos que cultivan soja en la población formada por todos los establecimientos del área en cuestión. Dicha frecuencia relativa es igual al cociente entre la frecuencia relativa de establecimientos que cultivan soja y maíz en toda la población y la frecuencia relativa de los establecimientos que cultivan soja en toda la población. Como las dos últimas frecuencias relativas corresponden, respectivamente, a los valores de la probabilidad conjunta de soja y maíz y de la probabilidad marginal de soja, podemos escribir a la probabilidad condicional como el siguiente cociente:

- Independencia estadística.

Dos eventos A y B son estadísticamente independientes si la probabilidad condicional de A dado B es igual a su probabilidad condicional dado B C . Si la probabilidad de que en un establecimiento tomado al azar se cultive maíz difiere según seleccionemos el establecimiento entre los cultivan soja o entre los que no cultivan soja, entonces se hace evidente cierta dependencia entre los eventos Maíz y Soja. Esto significa que podemos identificar a la independencia estadística como la igualdad entre dos probabilidades condicionales. Si los eventos Maíz y Soja fueran estadísticamente independientes, se tendría que cumplir que,

- Multiplicación

Para dos sucesos A y B, se define la probabilidad

Condicionada de A dado B como

Pr(A|B) = Pr(A y B)

Pr(B)

*Se entiende la expresión como la probabilidad de A suponiendo que B haya

Ocurrido.

A menudo se escribe esta fórmula de otra manera

Pr(A y B) = Pr(A|B) Pr(B).

En este caso, se le llama la ley de multiplicación:

Se dan dos cartas de una baraja española. ¿Cual es la probabilidad

de que ambas cartas sean copas?

Sea A (B) el suceso de que la primera (segunda) carta sea copa. Queremos

calcular Pr(A y B). Usamos la ley de multiplicación.

Pr(A y B) = Pr(B|A) Pr(A)

Tenemos que Pr(A) = 10/40 y Pr(B|A) = 9/39 porque si la primera carta es copa, quedan 39 cartas y nueve de ellas son copas.

Por tanto: Pr(A y B) = 1/ 40 × 9 /39 = 3 52 .

- Bayes

. Para dos sucesos A y B, se tiene

Pr(A|B) = Pr(B|A) Pr(A)

Pr(B)

Demostración

Por la regla de multiplicación, se tiene

·         Pr(A y B) = Pr(A|B) Pr(B) e igualmente

·         Pr(A y B) = Pr(B|A) Pr(A)                                                                                                                                     Pr(A|B) Pr(B) = Pr(B|A) Pr(A) y despejando obtenemos

Pr(A|B) = Pr(B|A) Pr(A)

Pr(B)

EJEMPLO:

Tres prisioneros, Alfredo, Bruno y Carlos han solicitado la libertad condicional. Se sabe que el gobernador va a poner en libertad a uno de los tres pero ´el no va a decir quien hasta finales del mes. El gobernador dice a Alfredo que puede informarle del nombre de un solicitante sin ´exito dadas las siguientes condiciones.

1. Si se va a liberar a Alfredo, el gobernador dirá Bruno o Carlos con la misma probabilidad (1/2).

2. Si se libera a Bruno, dirá el nombre de Carlos.

3. Si Carlos es el que se va a liberar, dirá Bruno.

Alfredo pide al gobernador que le diga el nombre y el gobernador creyendo que su información es inútil le dice que Bruno se va a quedar en la cárcel.

Alfredo piensa “mi probabilidad de que me pongan en libertad ha cambiado de 1/3 a 1/2. Estoy muy contento.” ¿Tiene razón?

·         Sean A, B,C los sucesos de que Alfredo, Bruno y Carlos respectivamente est´en puestos en libertad. Sea b el suceso de que el gobernador diga el nombre de Bruno.

Se tiene: Pr(A) = Pr(B) = Pr(C) = 1/3.

Además, sabiendo que el gobernador ha dicho el nombre de Bruno, se tiene

Pr(b|A) = 1/2, Pr(b|B) = 0, Pr(b|C) = 1.

Entonces, mediante el teorema de Bayes,

Pr(A|b) = Pr(b|A) Pr(A)

Pr(b)

=Pr(b|A) Pr(A)

Pr(b|A) Pr(A) + Pr(b|B) Pr(B) + Pr(b|C) Pr(C)

= 1/2 × 1/3

1/2 × 1/3 + 0 × 1/3 + 1 × 1/3= 1/3

CÁLCULO CON TÉCNICAS DE CONTEO

· Principio fundamental del conteo.  

El principio fundamental en el proceso de contar ofrece un método general para contar el numero de posibles arreglos de objetos dentro de un solo conjunto o entre carios conjuntos. Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.

Si un evento A puede ocurrir de n1 maneras y una vez que este ha ocurrido, otro evento B pueden2 maneras diferentes entonces, el número total de formas diferentes en que ambos eventos pueden ocurrir en el orden indicado, es igual a  n1 x n2.

·         ¿De cuántas maneras pueden repartirse 3 premios a un conjunto de 10 personas, suponiendo que cada persona no puede obtener más de un premio?

Aplicando el principio fundamental del conteo, tenemos 10 personas que pueden recibir el primer premio. Una vez que éste ha sido entregado, restan 9 personas para recibir el segundo, y posteriormente quedarán 8 personas para el tercer premio. De ahí que el número de maneras distintas de repartir los tres premios.

n

10 x 9 x 8 = 720

·         ¿Cuántas placas de automóvil se pueden hacer utilizando dos letras seguidas de tres cifras? No seadmiten repeticiones.

26 x 25 x 10 x 9 x 8 = 468000

Un  número entero positivo, el producto n (n-1) (n-2)...3 x 2 x 1 se llama factorial de n.

El símbolo! se lee factorial y es el producto resultante de todos los enteros positivos de 1 a n; es decir, sea 

n

5! = 5 x 4 x 3 x 2 x 1 = 120

Por definición 0! = 1

 Si el número de posibles resultados de un experimento es pequeño, es relativamente fácil listar y contar todos los posibles resultados. Al tirar un dado, por ejemplo, hay seis posibles resultados.

Si, sin embargo, hay un gran número de posibles resultados tales como el número de niños y niñas por familias con cinco hijos, sería tedioso listar y contar todas las posibilidades. Las posibilidades serían, 5 niños, 4 niños y 1 niña, 3 niños y 2 niñas, 2 niños y 3 niñas, etc.

 Para facilitar el conteo examinaremos  tres técnicas

* Diagrama de árbol.

* La técnica de la permutación

* La técnica de la combinación.

· Diagrama de árbol.

Un diagrama de árbol es una herramienta que se utiliza para determinar todos los posibles resultados de un experimento aleatorio. En el cálculo de la probabilidad se requiere conocer el número de elementos que forman parte del espacio muestral, estos se pueden determinar con la construcción del diagrama de árbol.El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta una serie de pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo. Se utiliza en los problemas de conteo y probabilidad.

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad. Cada una de esta ramas se conoce como rama de primera generación.

En el final de cada rama de primera generación se constituye a su vez, un nudo del cual parten nuevas ramas conocidas como ramas de segunda generación, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).Hay que tener en cuenta que la construcción de un árbol no depende de tener el mismo número de ramas de segunda generación que salen de cada rama de primera generación y que la suma de probabilidades de las ramas de cada nudo ha de dar 1.

EJEMPLO:

Calcular la probabilidad de que al arrojar al aire tres monedas, salgan 3 caras:

· Permutaciones.

la formula que se utiliza para contar el numero total de permutaciones distintas es:

                                               

                                              FÓRMULA: n P r = n! (n - r)

Ejemplo: ¿Como se puede designar los cuatro primeros lugares de un concurso, donde existen 15 participantes?

 Aplicando la formula de la permutación tenemos:                                                 

n P r = n! (n - r)! = 15! = 15*14*13*12 *11*10*9*8*7*6*5*4*3*2*1 (15-4)! 11*10*9*8*7*6*5*4*3*2*1 = 32760

1.       Donde: n= número total de objetos r= número de objetos seleccionados!= factorial, producto de los números naturales entre 1 y n.

2.      NOTA: se puede cancelar números cuando se tiene las mismas cifras en numerador y denominador. !

· Combinaciones.

En una permutación, el orden de los objetos de cada posible resultado es diferente. Si el orden de los objetos no es importante, cada uno de estos resultados se denomina combinación. Por ejemplo, si se quiere formar un equipo de trabajo formado por 2 personas seleccionadas de un grupo de tres (A, B y C). Si en el equipo hay dos funciones diferentes, entonces si importa el orden, los resultados serán permutaciones. Por el contrario si en el equipo no hay funciones definidas, entonces no importa el orden y los resultados serán combinaciones. Los resultados en ambos casos son los siguientes:

Permutaciones: AB, AC, BA, CA, BC, CB

Combinaciones: AB, AC, BC

Combinaciones: Es el número de formas de seleccionar r objetos de un grupo de n objetos sin importar el orden.

La fórmula de combinaciones es:

                     n C r = n!                        r! (n – r)!

EJEMPLO:

 En una compañía se quiere establecer un código de colores para identificar cada una de las 42 partes de un producto. Se quiere marcar con 3 colores de un total de 7 cada una de las partes, de tal suerte que cada una tenga una combinación de 3 colores diferentes. ¿Será adecuado este código de colores para identificar las 42 partes del producto?
Usando la fórmula de combinaciones:

n C r = n! = 7! = 7! = 35

r! (n – r )!  3! (7 – 3)!  3! 4!

El tomar tres colores de 7 posibles no es suficiente para identificar las 42 partes del producto.